
Забавные парадоксы, которые трудно осознать.
Человеческая логика — вещь действительно интересная. Она способна поставить в тупик даже саму себя. Именно этим уже не первое тысячелетие занимаются многочисленные мыслители, философы, ученые. Так уж повелось, что эти ребята очень любят «развлекать» себя вещами, которые при подключении упомянутой логики, не очень могут уложиться в голове даже самого незаурядного человека в плане интеллектуальных способностей.
1. Дихотомия Зенона

Греки любили думать о всяком.
Зенон Элейский, древнегреческий философ, пытался доказать, что утверждение о непрерывности и неограниченной делимости времени и пространства имеет серьезные проблемы с логикой.
Он утверждал, что для того, чтобы преодолеть путь, сначала нужно преодолеть половину пути. Для того, чтобы преодолеть половину, надо преодолеть ее половину. И так далее, и до бесконечности. Исходя из этого, Зенон утверждал, что движение не начнется (по этому принципу) никогда.
2. Стрела Зенона

Если хорошо подумать, то таки да.
Еще один логический шедевр от Зенона, с помощью которого он пытался познать движение. Несмотря на всю парадоксальность утверждения, именно благодаря ему в науке началась дискуссия о природе времени. Не закончена она и сейчас. А звучало все примерно так:
Летящая стрела неподвижна, потому как в каждый момент времени она занимает равное себе положение или иными словами покоится. И так как она покоится в каждый момент времени, то она покоится во все моменты времени, иначе не существует момента времени, когда бы она совершала движение.
3. Корабль Тесея

Все очень плохо для Тесея.
Парадокс очень прост. Звучит он следующим образом:
Если все составные части объекта были заменены, остается ли этот объект тем же объектом?
Описан сей парадокс был еще Плутархом, древнегреческим писателем и философом. Он был основан на размышлениях о корабле Тесея, на котором тот вернулся с Крита в Афины. Судно хранили несколько сотен лет и каждый год отправляли с посольством в Делос. Год от года при починке в корабле меняли доски, что и навело философов на такое размышление.
4. Парадокс всемогущества

Что если Бог, и не Бог.
Данный парадокс прост, и с его помощью философы обожают доказывать, что любой бог не может существовать. А звучит он вопросом: «Сможет ли всемогущее существо создать такой камень, который не сможет поднять?». И ответ «да», и ответ «нет» приводят к тому, что такое существо окажется не всемогущим.
5. Парадокс маляра

Только без воображения.
Звучит парадокс просто: фигура с бесконечной площадью поверхности может быть окрашена конечным количеством краски.
Для понимания нужно представить себе бесконечную ступенчатую пластинку. Пускай она состоит из прямоугольников. Первый из них – это квадрат со стороной 1 см. Каждый последующий при этом вдвое уже и вдвое длиннее предыдущего. В результате получается бесконечная площадь пластинки. Если вращать фигуру вокруг ее прямого края, то она станет объемной и будет состоять из цилиндров. Если посчитать, то ее объем станет равным 2*Пи см3, а значит, ее можно заполнить конечным количеством краски, погрузив бесконечную пластинку в сосуд.
6. Парадокс Греллинга — Нельсона

Хороший вопрос для учителя языка.
Представим, что в языке появились автологичные и гетерологичные прилагательные. Теперь все прилагательные выходят в эти два класса. При этом автологичные описывают только себя, а гетерологичные описывают только не себя.
Вопрос парадокса следующий: к какой категории тогда отнести слово «гетерологичный»? Так, если это автологичное прилагательное, то оно должно обладать обозначаемым свойством и станет в этом случае гетерологичным. Однако, если данное прилагательное гетерологичное, то названия у него быть не должно, а значит, оно не может, является тем, чем является.
7. Уловка-22

О ней даже написали книгу и сняли фильм.
Человек, который является сумасшедшим, может попросить об освобождении его от выполнения воинского долга. Однако всякий человек, который пытается уклониться от выполнения боевого долга по просьбе, не является подлинным сумасшедшим.
8. Парадокс интересных чисел

Забавно, не так ли?
«Один» – это первое ненулевое натуральное число. «Два» — это наименьше простое число. «Три» — это первое нечётное простое число. «Четыре» — это наименьшее составное число. Если продолжить мысль и разделить все натуральные числа на «интересные» и «не интересные», то получится, что все натуральные числа интересные.
Все потому, что если в математике существует непустое множество неинтересных натуральных чисел, то в нем будет наименьшее число. Наименьше неинтересное число – интересно, а значит, во всем этом есть противоречие.
9. Парадокс пьяницы

Пьют все.
Область формальной логики. Данный парадокс утверждает, что во всяком баре есть, по меньшей мере, один человек, для которого верно утверждение, что если пьет он, то пьют все. Теперь допустим, что в баре пьют все. Тогда для каждого человека верно описанное выше утверждение о том, что если пьет он, то пьют все. Если это неверно, то в баре есть, по меньшей мере, один человек, который не пьет. И так, так как теперь неверно то, что он пьет, то верно, что если он пьет, то пьют все.
10. Парадокс дружбы
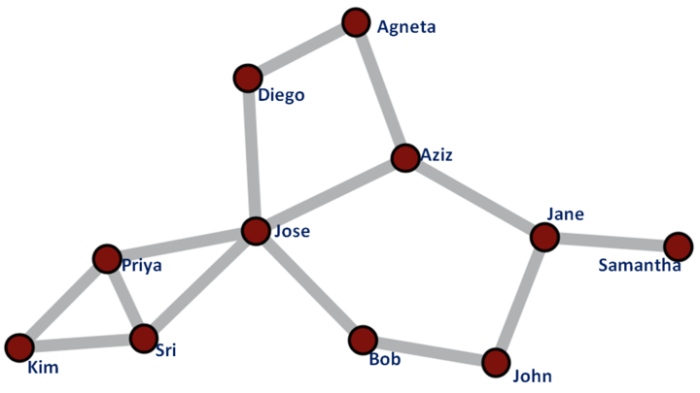
Теперь можно не расстраиваться.
Данный парадокс говорит о том, что у большинства людей друзей меньше, чем в среднем у их друзей. Хотя данное утверждение и звучит парадоксально, оно было математически обосновано. Логическое объяснение выводится из базовых принципов теории графов. Подтвердить его удалось в 2012 году.
В продолжение темы неожиданная причина, почему 95% женщин моет голову неправильно во всякое время.
Источник:

